Code
library(haven)
survival_data <- read_dta("survival_data.dta")
knitr::kable(survival_data[1:10, ], ) | studytime | died | group | age |
|---|---|---|---|
| 15 | 0 | 1 | 50 |
| 6 | 1 | 1 | 67 |
| 8 | 1 | 0 | 52 |
| 8 | 1 | 0 | 49 |
| 17 | 1 | 0 | 49 |
| 5 | 1 | 0 | 63 |
| 34 | 0 | 1 | 62 |
| 22 | 1 | 0 | 57 |
| 28 | 0 | 1 | 48 |
| 28 | 1 | 1 | 57 |
RLP
Como citar o conteúdo deste site
Pacheco RL, Martimbianco ALC, Riera, R. Interpretação de resultados de estudos clínicos e sínteses de evidências. 2022. Disponível em: www.nepsbeats.com.
Última atualização: 08/abril/2024.
Analisando um ensaio clínico randomizado em oncologia
No exemplo a seguir, examinaremos um ensaio clínico randomizado que possui o seguinte PICO:
P: Pacientes com carcinoma colorretal metastático
I: Imunoterapia + quimioterapia convencional
C: Placebo + quimioterapia convencional
O: Sobrevida globalA hipótese principal do estudo é a de que a imunoterapia aumenta a sobrevida de pacientes com carcinoma colorretal metastático. O estudo recrutou um total de 48 pacientes (20 no grupo placebo e 28 no grupo intervenção).
Base 1. Base de dados do ensaio clínico randomizado que avaliou imunoterapia em pacientes com carcinoma colorretal metastático.
| studytime | died | group | age |
|---|---|---|---|
| 15 | 0 | 1 | 50 |
| 6 | 1 | 1 | 67 |
| 8 | 1 | 0 | 52 |
| 8 | 1 | 0 | 49 |
| 17 | 1 | 0 | 49 |
| 5 | 1 | 0 | 63 |
| 34 | 0 | 1 | 62 |
| 22 | 1 | 0 | 57 |
| 28 | 0 | 1 | 48 |
| 28 | 1 | 1 | 57 |
As colunas significam:
studytime : tempo (em meses) até a censura ou evento
died: estado (vivo ou morto) do paciente no momento da censura
group: identificação de qual intervenção o paciente recebeu
age: idade do paciente no momento da randomização (linha de base)
A inspeção dos dados permite verificar, por exemplo, que o paciente 1 foi acompanhado por 15 meses e saiu do estudo precocemente. Os pacientes 2 e 3 morreram durante o acompanhamento (6 e 8 meses respectivamente).
Uma boa forma de captar a evolução de eventos ao longo do tempo é por meio de uma curva de sobrevida. O gráfico abaixo apresenta a curva de sobrevida do estudo pelo método de Kaplan-Meier.
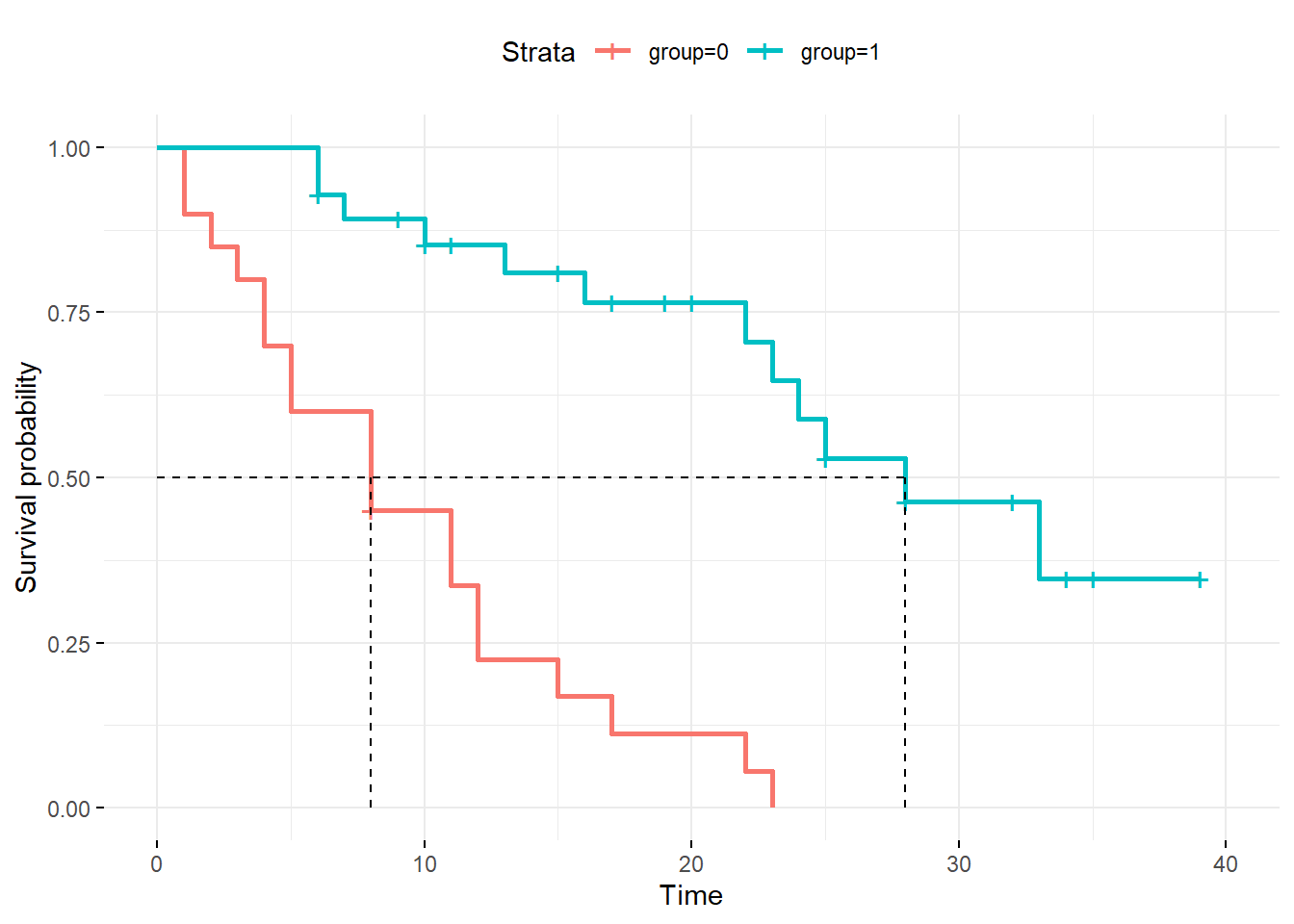
Em uma curva de sobrevida, o eixo X irá indicar a passagem de tempo, ou seja, o acompanhamento dos pacientes ao longo do estudo. Na curva apresentada, o eixo Y está indicando a proporção (%) de pacientes vivos. Quanto mais separadas as curvas, maior será a indicação de efeito da intervenção.
No tempo 0 meses (início do estudo), todos os pacientes estavam vivos. Pode-se notar que um pouco após os 20 meses, todos os pacientes do grupo placebo morreram ou abandonaram o estudo. Já no grupo intervenção, cerca de 35% dos pacientes ainda estavam vivos após 40 meses de seguimento do estudo.
Pela inspeção visual da curva de sobrevida, houve um grande distanciamento das curvas, o que parece indicar um benefício importante da intervenção no aumento da sobrevida.
Pode-se também adicionar uma tabela “at risk”, que indicará quantos pacientes ainda estavam em acompanhamento ao longo do seguimento. Nota-se que no início do estudo, todo tamanho amostral (48 pacientes) estavam em risco, e o número foi diminuindo ao longo do tempo.
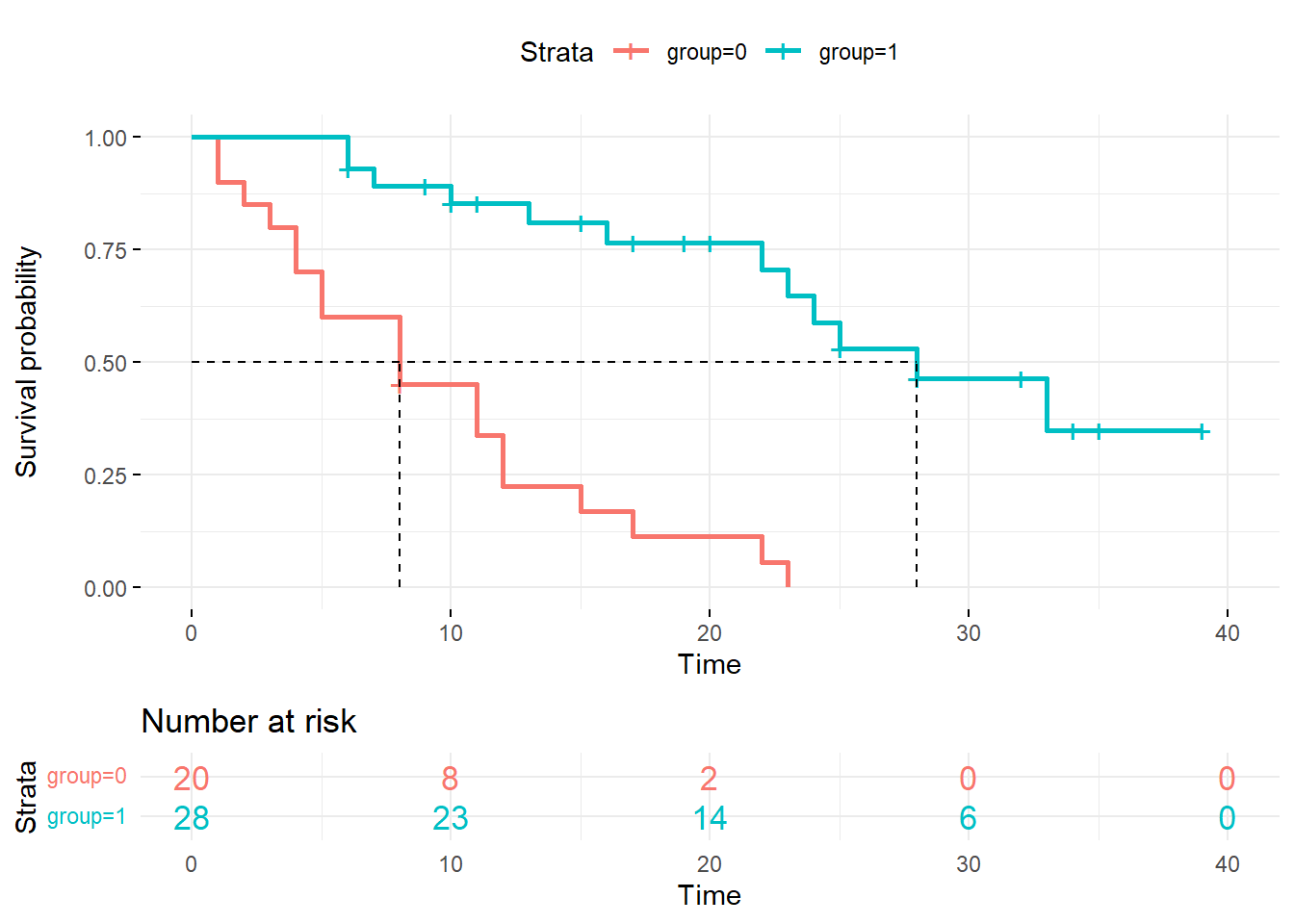
Figura 1. Curva de Kaplan-Meier com tabela “at risk”
Também é possível adicionar intervalos de confiança nas curvas de sobrevida, o que irá demonstrar a incerteza na separação das curvas (figura 2). No caso, é possível perceber uma importante separação das curvas, mesmo nos limites mais conservadores do intervalo de confiança.

Figura 2. Curva de Kaplan-Meier com tabela “at risk” e intervalos de confiança
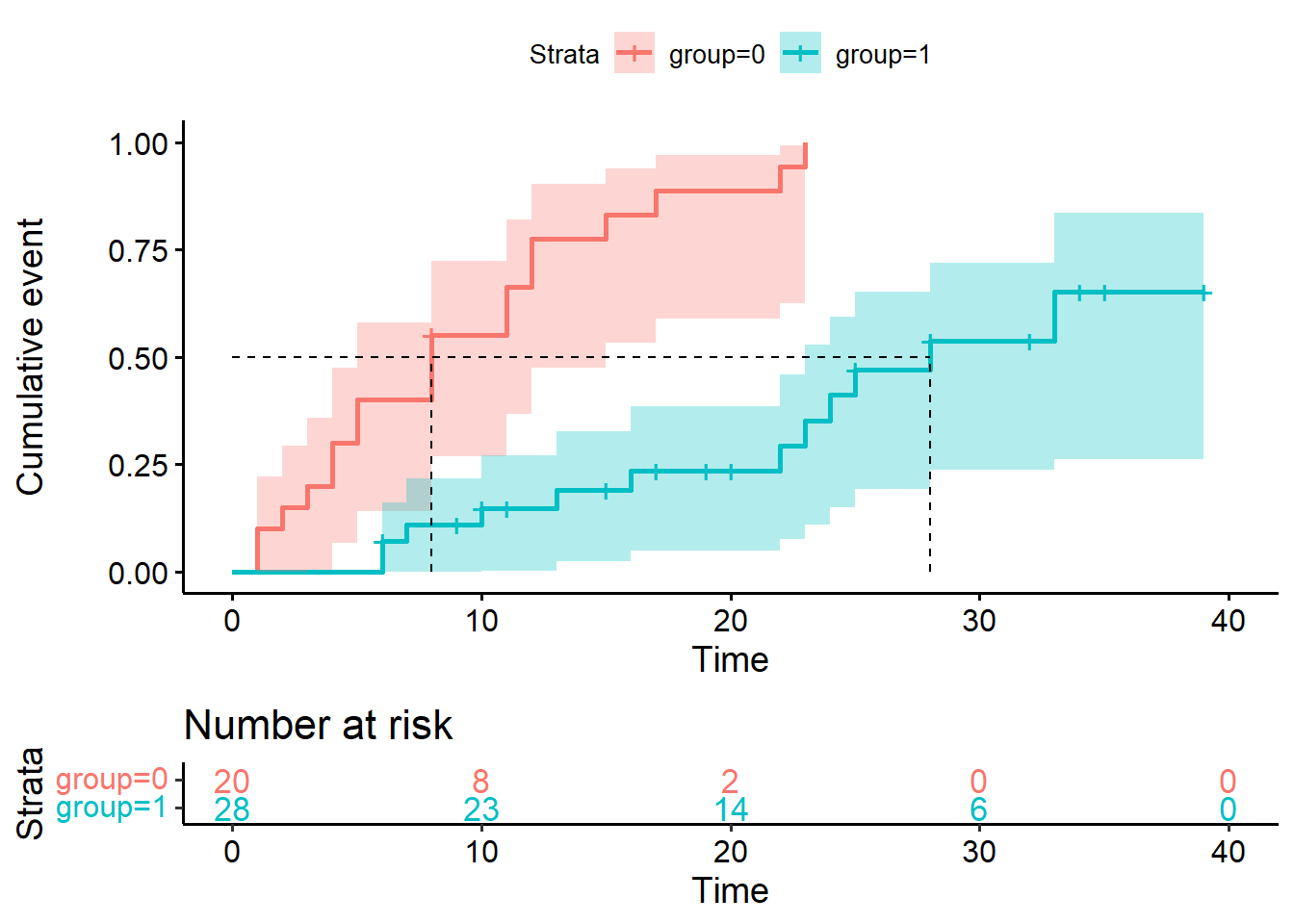
Uma outra forma de se apresentar curvas de sobrevida, seria inverter o Y para apresentação da proporção de pacientes que apresentaram o evento (figura 3).
Figura 3. Curva de sobrevida (proporção de pacientes com evento) e tabela at risk
A interpretação geral deve ser a mesma. No tempo 0 meses, 0% dos pacientes morreram. Um pouco além dos 20 meses, 100% dos pacientes do grupo placebo morreram.
A figura 3 apresenta a mesma informação da figura 1. A proporção de eventos no eixo Y geralmente é utilizada quando a taxa de eventos é baixa ao longo do estudo, pois há uma melhor visualização. No entanto, não existe certo e errado, pois a informação transmitida é a mesma.
A figura 4 apresenta os intervalos de confiança associados às curvas de mortalidade.
Figura 4. Curva de sobrevida (proporção de pacientes com evento) e tabela at risk e intervalos de confiança.
Com a apresentação gráfica das curvas de sobrevida, podemos ter vontade de afirmar que há efeito positivo da intervenção.
No entanto, ainda precisaremos de análises inferenciais mais robustas para chegar a esta conclusão, pois apenas a inspeção das imagens pode nos levar a conclusões errôneas. A regressão de Cox e a estimativa de hazard ratios são necessárias para nos ajudar a entender a magnitude do efeito da intervenção.
Back to top---
title: "Curvas de sobrevida"
author: RLP
format:
html:
code-fold: true
code-tools: true
css: style.css
editor_options:
chunk_output_type: inline
execute:
warning: false
---
**Como citar o conteúdo deste site**
Pacheco RL, Martimbianco ALC, Riera, R. Interpretação de resultados de estudos clínicos e sínteses de evidências. 2022. Disponível em: www.nepsbeats.com.
Última atualização: 08/abril/2024.
------------------------------------------------------------------------
***Analisando um ensaio clínico randomizado em oncologia***
No exemplo a seguir, examinaremos um ensaio clínico randomizado que possui o seguinte PICO:
```
P: Pacientes com carcinoma colorretal metastático
I: Imunoterapia + quimioterapia convencional
C: Placebo + quimioterapia convencional
O: Sobrevida global
```
A hipótese principal do estudo é a de que a imunoterapia aumenta a sobrevida de pacientes com carcinoma colorretal metastático. O estudo recrutou um total de 48 pacientes (20 no grupo placebo e 28 no grupo intervenção).
**Base 1**. Base de dados do ensaio clínico randomizado que avaliou imunoterapia em pacientes com carcinoma colorretal metastático.
```{r}
library(haven)
survival_data <- read_dta("survival_data.dta")
knitr::kable(survival_data[1:10, ], )
```
As colunas significam:
```
studytime : tempo (em meses) até a censura ou evento
died: estado (vivo ou morto) do paciente no momento da censura
group: identificação de qual intervenção o paciente recebeu
age: idade do paciente no momento da randomização (linha de base)
```
A inspeção dos dados permite verificar, por exemplo, que o paciente 1 foi acompanhado por 15 meses e saiu do estudo precocemente. Os pacientes 2 e 3 morreram durante o acompanhamento (6 e 8 meses respectivamente).
Uma boa forma de captar a evolução de eventos ao longo do tempo é por meio de uma curva de sobrevida. O gráfico abaixo apresenta a curva de sobrevida do estudo pelo método de Kaplan-Meier.
```{r}
library(survival)
library(survminer)
s1 <- survfit(Surv(studytime, died) ~ group, data = survival_data)
ggsurvplot(s1,
surv.median.line = "hv",
ggtheme = theme_minimal())
```
Em uma curva de sobrevida, o eixo X irá indicar a passagem de tempo, ou seja, o acompanhamento dos pacientes ao longo do estudo. Na curva apresentada, o eixo Y está indicando a proporção (%) de pacientes vivos. Quanto mais separadas as curvas, maior será a indicação de efeito da intervenção.
No tempo 0 meses (início do estudo), todos os pacientes estavam vivos. Pode-se notar que um pouco após os 20 meses, todos os pacientes do grupo placebo morreram ou abandonaram o estudo. Já no grupo intervenção, cerca de 35% dos pacientes ainda estavam vivos após 40 meses de seguimento do estudo.
Pela inspeção visual da curva de sobrevida, houve um grande distanciamento das curvas, o que **parece indicar** um benefício importante da intervenção no aumento da sobrevida.
Pode-se também adicionar uma tabela *“at risk”*, que indicará quantos pacientes ainda estavam em acompanhamento ao longo do seguimento. Nota-se que no início do estudo, todo tamanho amostral (48 pacientes) estavam em risco, e o número foi diminuindo ao longo do tempo.
```{r}
library(survminer)
ggsurvplot(s1,
risk.table = TRUE,
risk.table.col = "group",
surv.median.line = "hv",
ggtheme = theme_minimal())
```
**Figura 1.** Curva de Kaplan-Meier com tabela *“at risk”*
Também é possível adicionar intervalos de confiança nas curvas de sobrevida, o que irá demonstrar a incerteza na separação das curvas (**figura 2**). No caso, é possível perceber uma importante separação das curvas, mesmo nos limites mais conservadores do intervalo de confiança.
```{r}
library(survminer)
ggsurvplot(s1,
conf.int = TRUE,
risk.table = TRUE,
risk.table.col = "group",
surv.median.line = "hv",
ggtheme = theme_minimal())
```
**Figura 2.** Curva de Kaplan-Meier com tabela *“at risk”* e intervalos de confiança
Uma outra forma de se apresentar curvas de sobrevida, seria inverter o Y para apresentação da proporção de pacientes que apresentaram o evento (**figura 3**).
```{r}
library(survminer)
ggsurvplot(s1,
surv.median.line = "hv",
fun = "event")
```
**Figura 3.** Curva de sobrevida (proporção de pacientes com evento) e tabela *at risk*
A interpretação geral deve ser a mesma. No tempo 0 meses, 0% dos pacientes morreram. Um pouco além dos 20 meses, 100% dos pacientes do grupo placebo morreram.
A **figura 3** apresenta a mesma informação da **figura 1**. A proporção de eventos no eixo Y geralmente é utilizada quando a taxa de eventos é baixa ao longo do estudo, pois há uma melhor visualização. No entanto, não existe certo e errado, pois a informação transmitida é a mesma.
A **figura 4** apresenta os intervalos de confiança associados às curvas de mortalidade.
**Figura 4.** Curva de sobrevida (proporção de pacientes com evento) e tabela *at risk* e intervalos de confiança.
```{r}
library(survminer)
ggsurvplot(s1,
conf.int = TRUE,
risk.table = TRUE,
risk.table.col = "group",
surv.median.line = "hv",
fun = "event")
```
Com a apresentação gráfica das curvas de sobrevida, podemos ter vontade de afirmar que há efeito positivo da intervenção.
No entanto, ainda precisaremos de análises inferenciais mais robustas para chegar a esta conclusão, pois apenas a inspeção das imagens pode nos levar a conclusões errôneas. A regressão de Cox e a estimativa de *hazard ratios* são necessárias para nos ajudar a entender a magnitude do efeito da intervenção.